Section 18: Problem 7 Solution

Working problems is a crucial part of learning mathematics. No one can learn topology merely by poring over the definitions, theorems, and examples that are worked out in the text. One must work part of it out for oneself. To provide that opportunity is the purpose of the exercises.

James R. Munkres

(a) Suppose that $f:\mathbb{R}\rightarrow\mathbb{R}$ is "continuous from the right," that is, $\lim_{x\rightarrow a^{+}}f(x)=f(a),$ for each $a\in\mathbb{R}$ . Show that $f$ is continuous when considered as a function from $\mathbb{R}_{l}$ to $\mathbb{R}$ .

(b) Can you conjecture what functions $f:\mathbb{R}\rightarrow\mathbb{R}$ are continuous when considered as maps from $\mathbb{R}$ to $\mathbb{R}_{l}$ ? As maps from $\mathbb{R}_{l}$ to $\mathbb{R}_{l}$ ? We shall return to this question in Chapter 3.

When we make the topology of the domain finer, there are, in general, more continuous functions, as some preimages of open sets that were not open can now become open. Similarly, we may have more continuous functions if we make the topology of the range coarser. The opposite is true if we make the topology of the domain coarser or the topology of the range finer, i.e. in these cases some continuous functions may become not continuous. However, when we make both domain and range finer (or coarser) at the same time, the set of continuous functions may change unpredictably. After all, if both domain and range have indiscrete topology, every function is continuous, but the same is true if both have the discrete topology. So, while changing the topology from one to the other, we may first loose some continuous functions but then gain them again.

In our case, this means that we expect all standard (i.e. as a function from $\mathbb{R}$ to $\mathbb{R}$ ) continuous functions to be continuous when considered as functions from $\mathbb{R}_{l}$ to $\mathbb{R}$ (the domain is strictly finer), and we can have more continuous functions (according to (a) all continuous from the right functions become continuous in these topologies). However, not every standard continuous function is going to be continuous as a function from $\mathbb{R}$ to $\mathbb{R}_{l}$ . Of course, all constant functions are still going to be continuous. But are there any others? And in the case of functions from $\mathbb{R}_{l}$ to $\mathbb{R}_{l}$ , we cannot even say (without further investigation) whether any standard continuous function is still going to be continuous, or whether there going to be any new continuous functions.

(a) If $V$ is open in $\mathbb{R}$ and $x\in f^{-1}(V)$ then $y=f(x)\in V$ , and for some $\delta>0$ , $(y-\delta,y+\delta)\subset V$ . Therefore, $\exists\epsilon>0$ such that $f([x,x+\epsilon))\subset(y-\delta,y+\delta)\subset V$ and $[x,x+\epsilon)\subset f^{-1}(V)$ . Thus, $f^{-1}(V)$ is open in $\mathbb{R}_{l}$ .

In fact, the opposite is also true. Indeed, if $f:\mathbb{R}_{l}\rightarrow\mathbb{R}$ is continuous, then for every $\delta>0$ , $I=(f(x)-\delta,f(x)+\delta)$ is open, $f^{-1}(I)$ is open and contains $x$ , there is a basis element $[x,x+\epsilon)$ such that $[x,x+\epsilon)\subset f^{-1}(I)$ , hence, $f([x,x+\epsilon))\subset I$ . So, we can say that a function is continuous from the right iff it is continuous as a function from $\mathbb{R}_{l}$ to $\mathbb{R}$ .

(b) From $\mathbb{R}$ to $\mathbb{R}_{l}$ only constant functions are continuous. Indeed, the inverse image of any $[a,b)$ has to be both open and closed, and there are only two such sets in $\mathbb{R}$ , namely, the empty set and $\mathbb{R}$ .

Now, from $\mathbb{R}_{l}$ to $\mathbb{R}_{l}$ . $f:\mathbb{R}_{l}\rightarrow\mathbb{R}_{l}$ is continuous iff for every $x\in\mathbb{R}$ and $\delta>0$ , there exists $\epsilon>0$ such that $f([x,x+\epsilon))\subset[f(x),f(x)+\delta)$ . This can be proved exactly the same way as we did in (a). Now, what this $\epsilon-\delta$ definition of continuity means... $f$ must be continuous from the right and locally non-decreasing from the right.

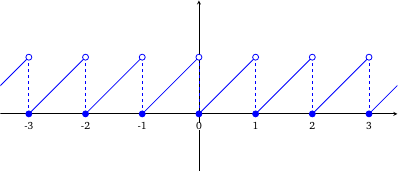
As we noted in the beginning, indeed, in this case some standard continuous functions are not continuous anymore (for example, the strictly decreasing $f(x)=-x$ where $f^{-1}([0,1))=(-1,0]$ is not open), but we also have some new continuous functions, such as the one shown in Figure 1↓. The function also illustrates that a “locally non-decreasing from the right” function does not have to be non-decreasing (from both sides) even locally.

Figure 1 A continuous function from $\mathbb{R}_{l}$ to $\mathbb{R}_{l}$ .

figure a_continuous_function_from_Rl_to_Rl.png

Subpages

Section 18: Problem 7 Solution

Section 18: Problem 7 Solution