$p$ is continuous and surjective. For each $z\in Z$ there is an open neighborhood $U$ of $z$ evenly covered by $r$ , that is $r^{-1}(U)$ is the union of disjoint open sets $U_{i}$ in $Y$ each homeomorphic to $U$ where $r|_{U_{i}}$ is a homeomorphism. Further, let $z_{i}\in U_{i}$ be such that $r(z_{i})=z$ . There is an open neighborhood $V_{i}$ of $z_{i}$ evenly covered by $q$ . Then $r(V_{i})$ is open in $Z$ ($r$ is an open map, see the last paragraph on page 336) and $z=r(z_{i})\in r(V_{i})\cap r(U_{i})=r(V_{i})\cap U$ . Since there are finite number of $z_{i}$ ’s, $U'=\cap_{i}r(V_{i})\cap U$ is an open neighborhood of $z$ .

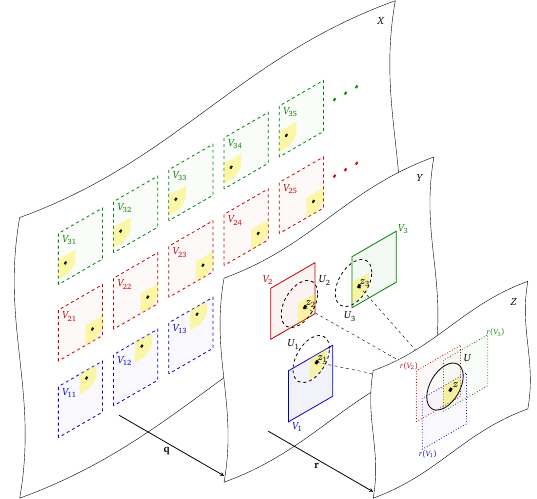
We claim that $U'$ is evenly covered by $p$ . Indeed, since $U$ is evenly covered by $r$ , $U'$ , as an open subset of $U$ , is evenly covered by $r$ where slices are $U'_{i}=r^{-1}(U')\cap U_{i}$ ($r^{-1}(U')\subset r^{-1}(U)$ $=\cup_{i}U_{i}$ and $r|_{U_{i}}$ is a homeomorphism for each $i$ ). Further, for every $i$ , $U'_{i}\subset V_{i}\cap U_{i}$ (because $r|_{U_{i}}$ is a homeomorphism and $U'\subset r(U_{i})\cap r(V_{i})$ ), i.e. $U'_{i}$ is an open subset of $V_{i}$ evenly covered by $q$ , hence, $U'_{i}$ is evenly covered by $q$ (similar argument as above for $U'$ ). Note that if $i\neq j$ , the slices of $q^{-1}(U'_{i})$ and $q^{-1}(U'_{j})$ are disjoint, because $U'_{i}\subset U_{i}$ and $U'_{j}\subset U_{j}$ where $U_{i}$ and $U_{j}$ are disjoint. Overall, $p^{-1}(U')=\cup_{i}q^{-1}(U'_{i})=\cup_{i}U'_{ij}$ is the disjoint union of open subsets of $X$ , where each $U'_{ij}$ is homeomorphic to $U'$ via the corresponding $U'_{i}$ , and $p|_{U'_{ij}}=r|_{U'_{i}}\circ q|_{U'_{ij}}$ is a homeomorphism. See Figure 1↓.