Section 13: Problem 4 Solution
Working problems is a crucial part of learning mathematics. No one can learn topology merely by poring over the definitions, theorems, and examples that are worked out in the text. One must work part of it out for oneself. To provide that opportunity is the purpose of the exercises.
James R. Munkres
(a) If
is a family of topologies on
, show that
is a topology on
. Is
a topology on
?
(b) Let
be a family of topologies on
. Show that there is a unique smallest topology on
containing all the collections
, and a unique largest topology contained in all
.
(c) lf
, let
Find the smallest topology containing
and
, and the largest topology contained in
and
.
(a) The empty set,
, unions of sets from
and their finite intersections all lie in every topology
(because every set from
belongs to every
), and, therefore, they all are contained in
.
At the same time, the union
does not have to be a topology. For example, the union of topologies
and
on
is not a topology, as it is missing the union of the sets
and
, i.e.
.
(b) The unique largest topology contained in all the topologies of the family
is clearly the intersection of the topologies
(it is the largest collection of sets contained in all
, and it is a topology according to (a)).
The smallest topology containing all the topologies of the family
can be obtained in two different ways.
First, we can consider all the topologies containing each
, and take their intersection. The resulting collection of sets is the smallest topology (by (a)) containing every
.
Second, we will prove in Exercise 5, that the smallest topology containing every set from a collection of sets is the one generated by the collection as a subbasis (in general, we may need to include the whole space as a set into the collection, so that it would be indeed a subbasis, but in our case each
is already a topology). So, accordingly, we consider
as a subbasis for a topology, and then it generates the smallest topology containing every
.
The first approach is less constructive (as it operates with the family of all topologies containing every topology
without specifying how to obtain it), but it is more general, as whenever we need to find the smallest set satisfying property
that contains every set
, the first thing to do is to check whether the intersection of all sets satisfying
and containing every
, satisfies
. If it does (as in our case, where
is “being a topology”), then the intersection is automatically the smallest such set.
The second approach, at the same time, is more constructive, as it prescribes exactly how to obtain a subbasis for the smallest topology, but it requires additional proof to show that the resulting topology is indeed the smallest (see Exercise 5).
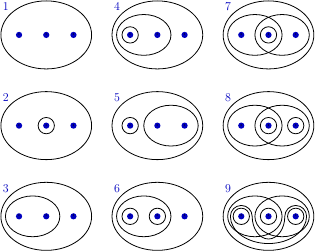
(c) The following Figure 1↓ lists the topologies of Figure 12.1.
The topologies we are asked about are the topologies 4 and 5. Their intersection is the largest topology contained in both, it is the topology
(the topology 2 where the central point is
). Their union
is a subbasis for the smallest topology containing both, all possible intersections of these sets gives as a basis for the topology, which is
. In fact, the set is closed under unions, so it is already the smallest topology containing both topologies (the topology 8 where the left point is
).
Note, that if we used the other method to obtain the smallest topology containing both given topologies, we would have to consider all 29 three-element topologies, including those that are not present in the picture above, check which ones contain both topologies given, and then take their intersection. With three elements this at least looks manageable, but the number of topologies grows as
with the number of elements
, and the exact number of topologies is unknown for even small values of
. Imagine if our topologies were infinite, or if there were an infinite number of them. This is exactly what I meant when I said that the first method is less constructive.