Section 13: Problem 2 Solution

Working problems is a crucial part of learning mathematics. No one can learn topology merely by poring over the definitions, theorems, and examples that are worked out in the text. One must work part of it out for oneself. To provide that opportunity is the purpose of the exercises.

James R. Munkres

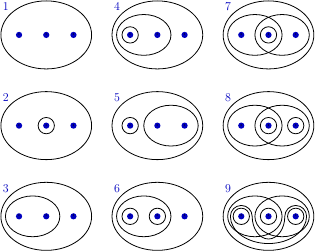
Consider the nine topologies on the set $X=\{a,b,c\}$ indicated in Example 1 of §12. Compare them; that is, for each pair of topologies, determine whether they are comparable, and if so, which is the finer.

Let us enumerate the topologies by columns, as shown in Figure 1↓.

Figure 1 Three element topologies.

Let " $\prec$ " be the partial relation between any two topologies that indicates that the topology on the left side is coarser (smaller) than the topology on the right side. Here we list all maximal ordered subsets of the set of topologies of Example 1 of §12 ordered by " $\prec$ ": $1\prec2\prec6\prec9$ , $1\prec2\prec7\prec8\prec9$ , $1\prec3\prec4\prec6\prec9$ , $1\prec3\prec7\prec8\prec9$ , and $1\prec5\prec9$ .

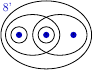
Note, that out of 29 possible topologies on the set of three elements, only 9 are shown here (because every other topology can be obtained from one of these by permutating its elements). However, this does not mean that such permutations preserve relations stated above. For example, if instead of the set 8 we had the set shown in Figure 2↓, we would additionally have

, i.e. $1\prec3\prec4\prec6\prec8'\prec9$ .

figure another_three_element_topology.png

Figure 2 Another three element topology.

Subpages

Section 13: Problem 2 Solution

Section 13: Problem 2 Solution