Section 13: Basis for a Topology

• Alternatively, it is the collection of all unions of basis elements (together with the empty set).
• It is also the smallest topology containing the basis.

• Alternatively, $\mathcal{B}$ is a basis for $\mathcal{T}$ iff $\mathcal{B}\subset\mathcal{T}$ and every open set is the union of some elements of $\mathcal{B}$ .

• The topology generated by $\mathcal{B}'$ is finer than $\mathcal{T}$ (or, respectively, the one generated by $\mathcal{B}$ ) iff every open set of $\mathcal{T}$ (or, respectively, basis element of $\mathcal{B}$ ) can be represented as the union of some elements of $\mathcal{B}'$ .

1. A subbasis $\mathcal{S}$ for a topology on $X$ is a collection of subsets of $X$ such that $X$ equals their union. The topology generated by the subbasis $\mathcal{S}$ is generated by the collection of finite intersections of sets in $\mathcal{S}$ as a basis (it is also the smallest topology containing the subbasis).
2. The intersection of any collection of topologies is a topology (the largest topology contained in all the topologies in the collection), while the union even of two topologies may be just a subbasis for a topology (the smallest topology containing all the topologies in the collection).

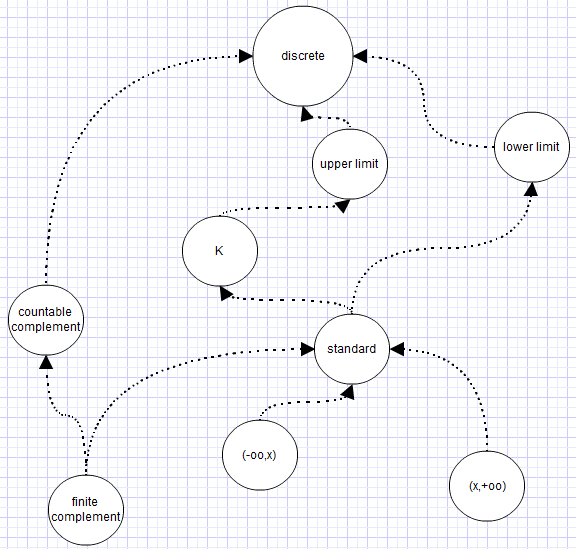
Real line topologies

1. $\mathbb{R}$ is the real line given the standard topology generated by intervals $()$ .
2. $\mathbb{R}_{l}$ is the real line given the lower limit topology generated by intervals $[)$ .
3. $\mathbb{R}_{u}$ is the real line given the upper limit topology generated by intervals $(]$ .
4. $\mathbb{R}_{d}$ is the real line given the discrete topology generated by intervals $[]$ or, alternatively, by singletons.
5. $\mathbb{R}_{fc}$ is the real line given the finite compliment topology.
6. $\mathbb{R}_{cc}$ is the real line given the countable compliment topology.
7. $\mathbb{R}_{K}$ is the real line given the K-topology generated by intervals $()$  and sets of the form $()-K$ where $K=\{1/n|n\in\mathbb{Z}_{+}\}$ .
8. $\mathbb{R}_{-\infty}$ is the real line given the topology generated by intervals $(-\infty,x)$ .
9. $\mathbb{R}_{+\infty}$ is the real line given the topology generated by intervals $(x,+\infty)$ .

Figure 1 Finer/coarser relations among topologies on $\mathbb{R}$ .